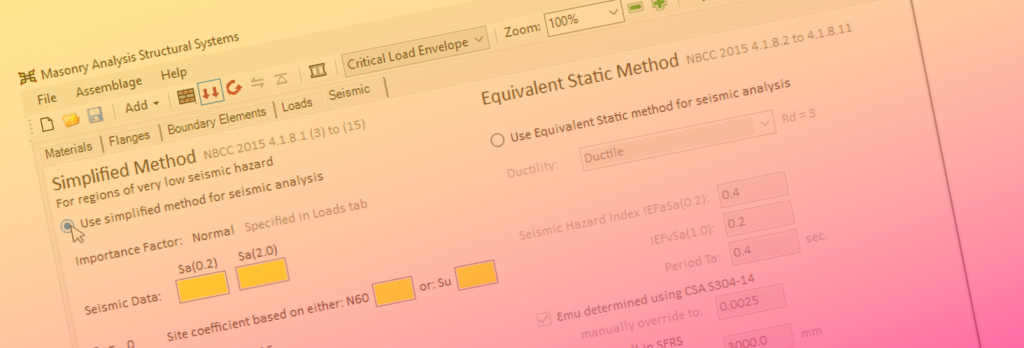
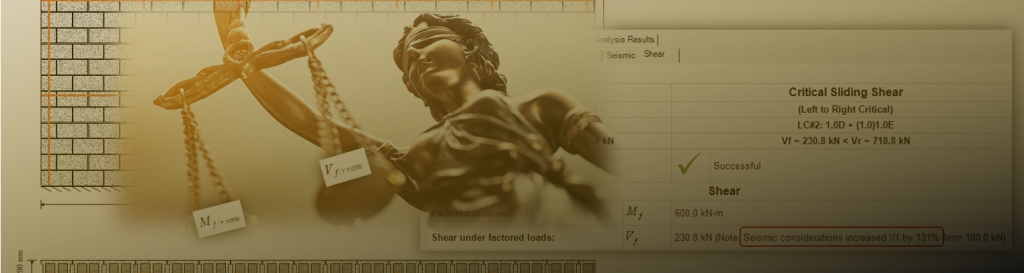
Taking seismic effects into account in MASS can be confusing. Seeing factored shear forces scaled up by over 100% in some cases may seem larger than expected.

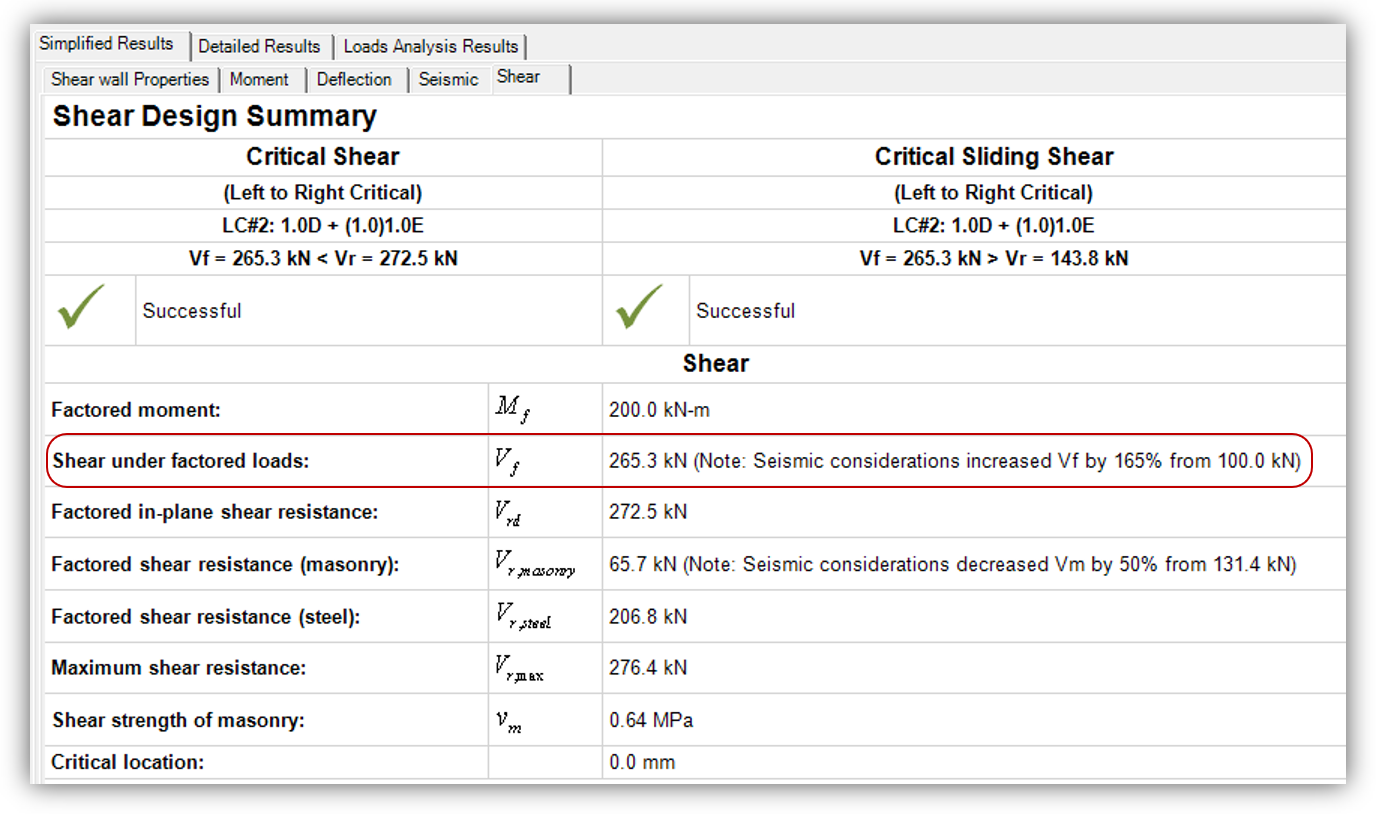
The main post found here outlines the clauses being invoked here where the requirements are broken down into two parts: (a) and (b). This post is followed up by a multi-storey example, illustrating the same concept, linked here.

Disclaimer: This post is exclusively intended to provide insight into the approach taken by the MASS design software in interpreting a CSA S304-14 code compliant seismic design. It is up to the professional discretion of the designer to input an appropriate layout, boundary and loading conditions, interpret the results, and determine how they should be incorporated into their designs. As per the end user license agreement (and also recommended within PEO’s guidelines for using engineering software), a tool cannot be considered competent and reliance on a tool does not relieve the user of responsibility.

For referenced, as covered in the main post linked here, the requirements for in-plane shear design can be broken down into two parts. The subsequent concept section outlines part (a) followed by an example demonstrating both parts (a) and (b).

General Concept of Part (a)

Looking at a conventional construction shear wall, the in-plane shear must be performed in accordance with CSA S304-14: 16.5.4:

Note that conventional construction was shown here because it is used for the example problem further down. There are additional CSA S304-14 references for each reinforced SFRS category which is explained in the main seismic shear post, linked here. Only part (a) is explained in this section with part (b) checked in the example problem further down.

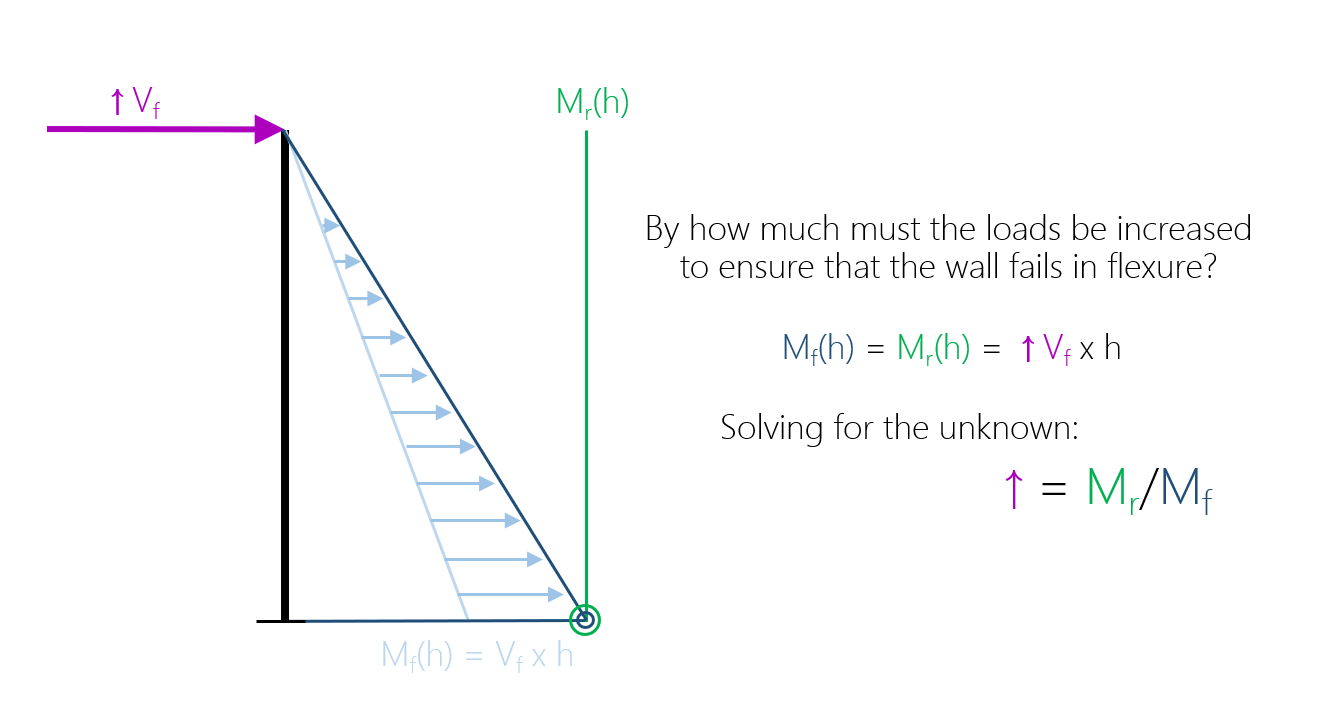
Simplifying things down to a basic cantilever shear wall element with a lateral load applied at the top, bending moment is experienced along the height with the highest magnitude occurring at the base. Assuming that the shear wall has adequate flexural capacity to resist the factored loading, the moment resistance further to the right, representing a constant, higher magnitude.

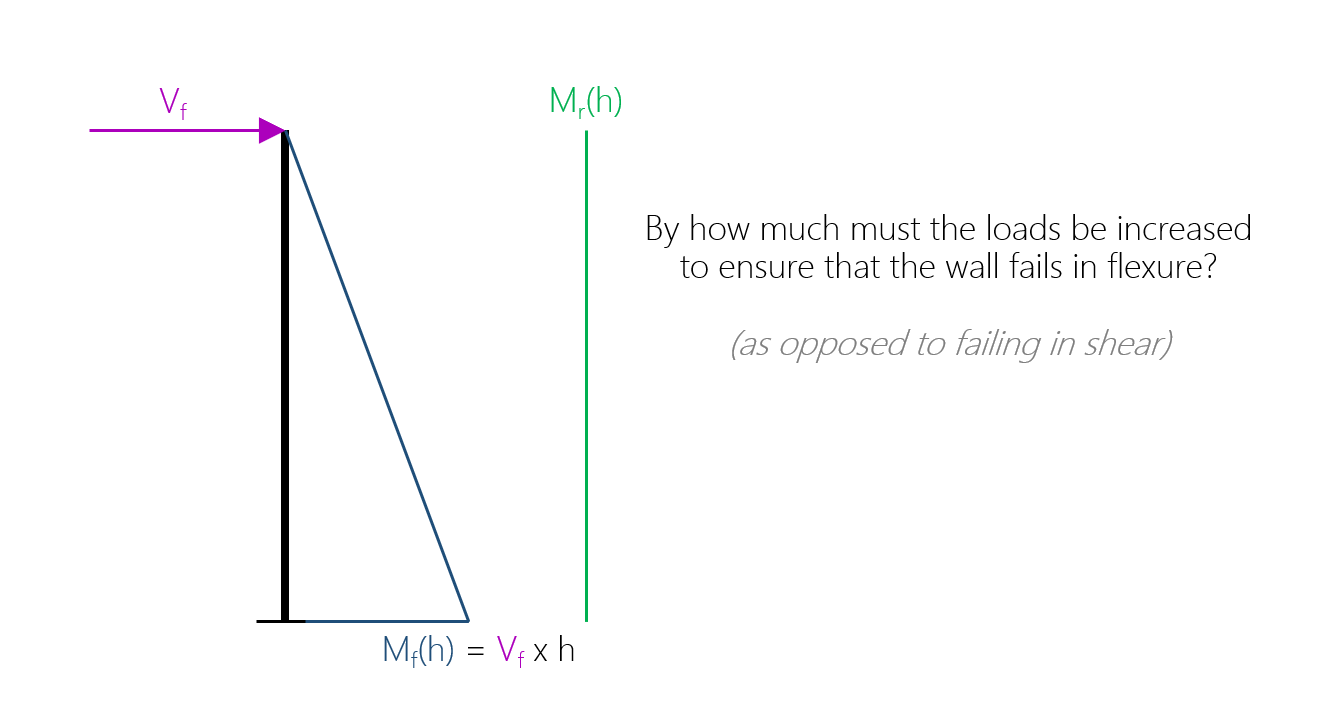
Note: Moment resistance, M_r, is shown as constant along the height, whereas technically this value changes slightly due to increasing axial loads resulting from self-weight supported above the section in question. Since the governing moment is shown at the base of the wall, the corresponding resistance at that location is shown for the full height. For shear walls, this variation is typically very small.

To ensure a ductile flexural failure mechanism occurs (as opposed to a sudden shear failure), the shear wall can be designed for an amplified in-plane factored shear that corresponds to the shear wall failing in flexure. The more difficult question is by how much does the shear force need to be increased by?

Another way to picture this problem is to imagine the lateral load being increased gradually until the highest occurring factored moment reaches the moment resistance. The factored shear force caused by that increased applied loading is the value that can be designed for when evaluating a shear wall’s in-plane shear resistance.

This increase can be solved for as a ratio of a shear wall’s moment resistance to factored moment ratio, shown below:

Substituting this ratio into the force and corresponding factored shear force, the expression for V_f,seismic is shown below: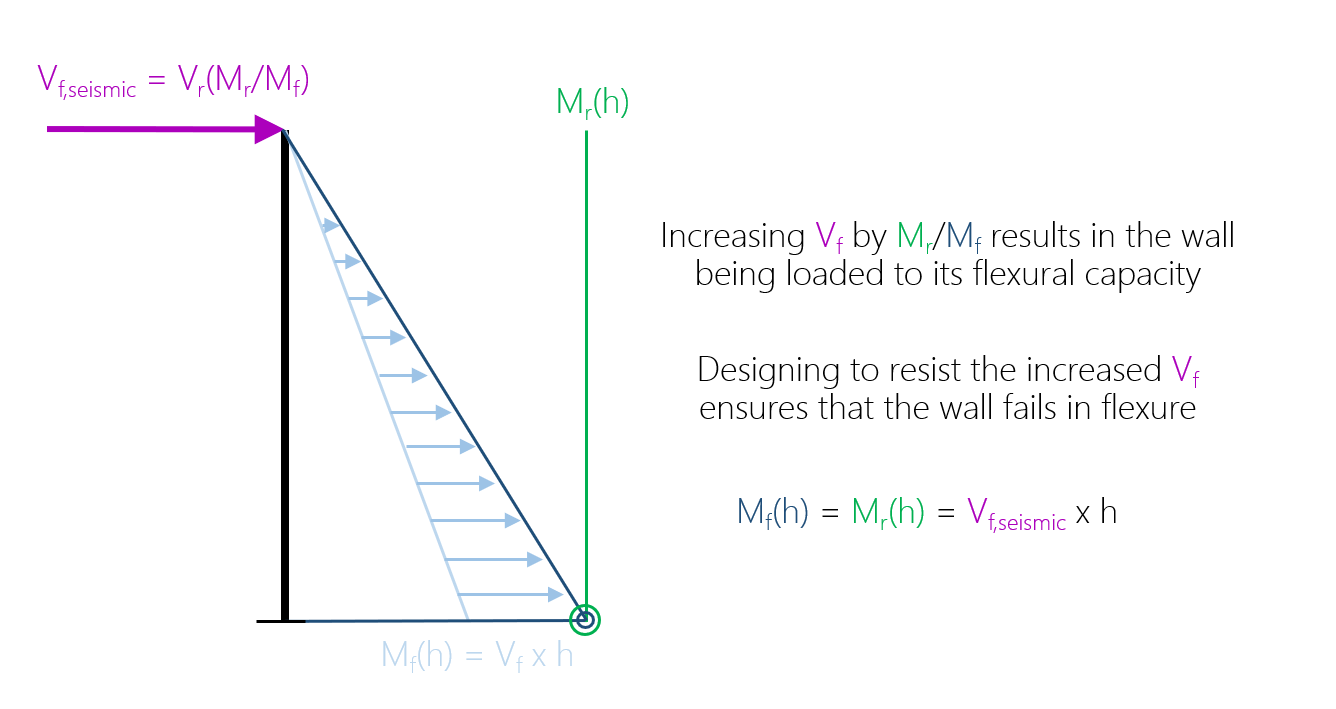

Recall that this is only considering the first part of the CSA Standards and does not also consider the limit considering overstregnth and ductility SFRS force modification factors. V_f,seismic need only be taken as the lesser of these two limits, explained further in the main post covering this topic, linked here.

Seismic Shear Example

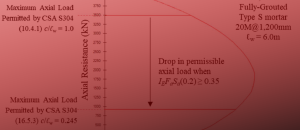
Consider a shear wall element that is 4 m in height and has an earthquake type lateral load applied at the top of 250 kN, pictured below. It’s cross section has a moment resistance of 1500 kN·m, which is 33% greater than the factored moment experienced at the base.

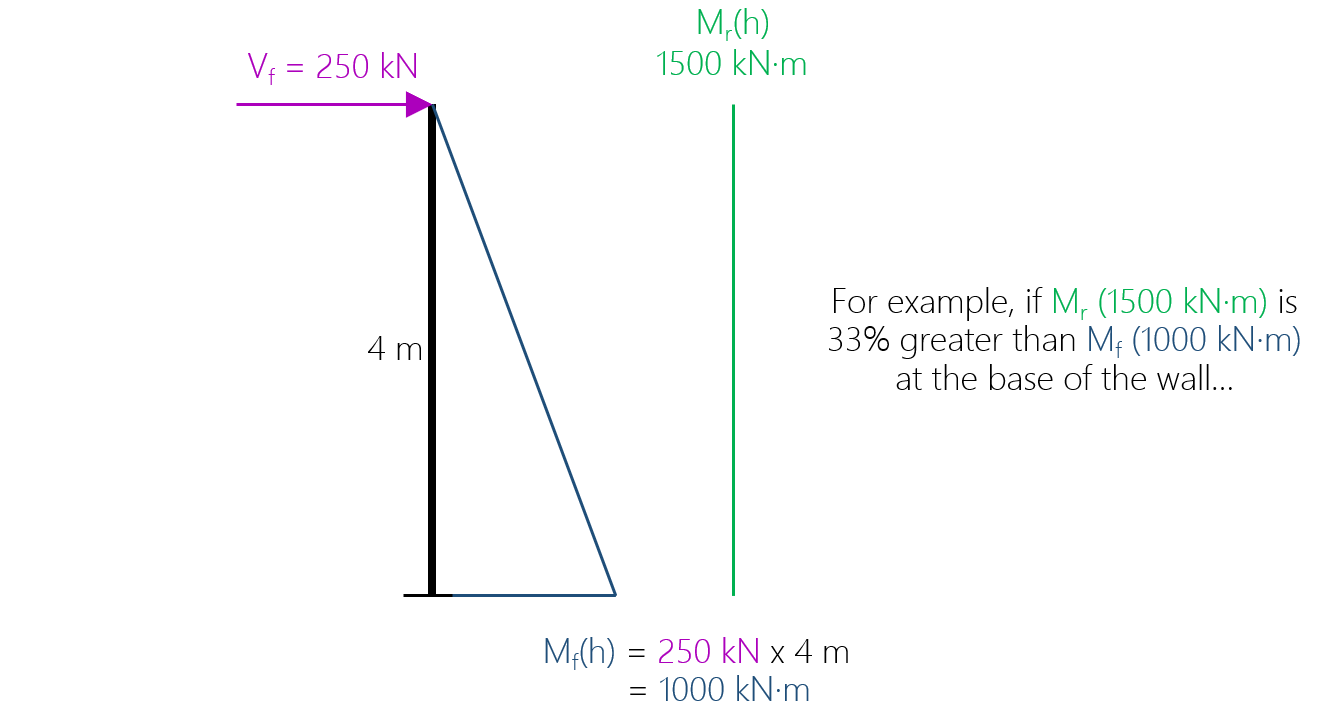
The resulting ratio of moment resistance to factored moment is 1.5, which can be used to scale up the applied load and factored shear.

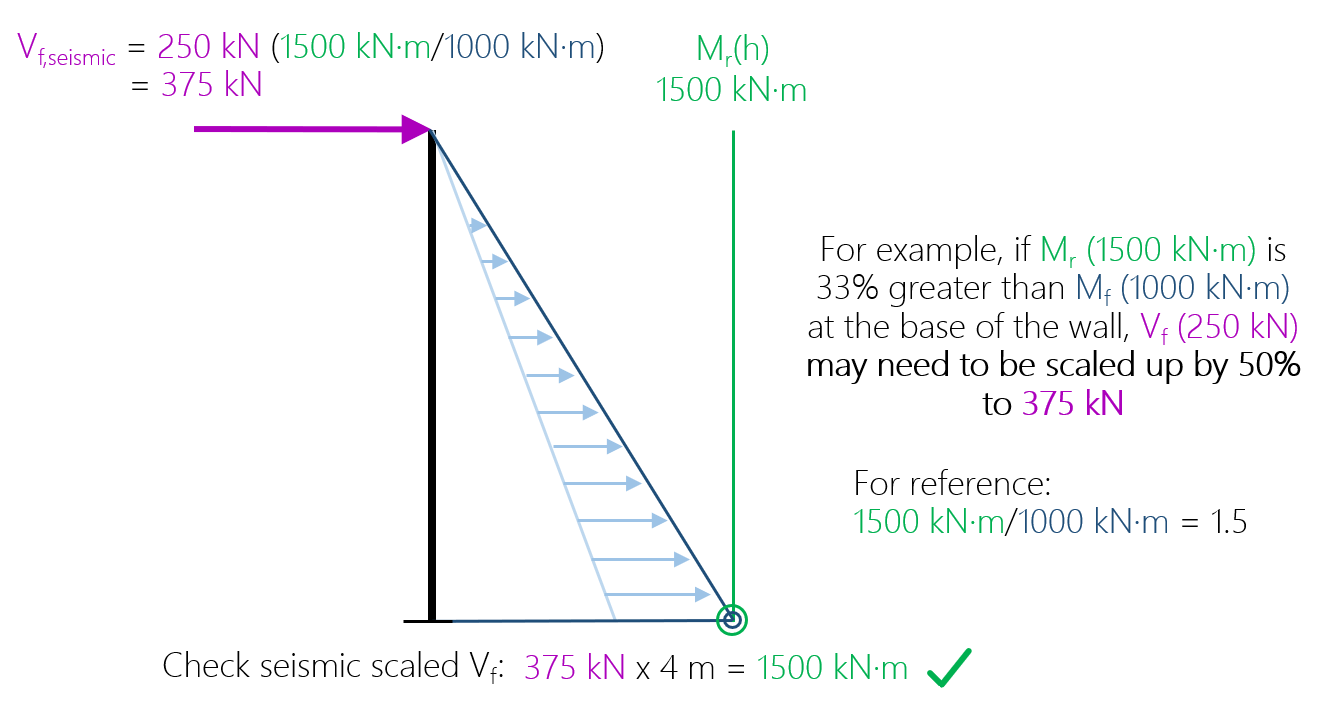
As a result, V_f,seismic is calculated to be 375 kN. Designed the shear wall to have an in-plane resistance higher than 375 kN ensures a ductile failure mechanism (flexure). Whether or not 375 kN is the magnitude needed to satisfy CSA S304-14: 16.5.4 depends on the limit outlined in part (b).

Checking against the limit from part (b)

It is the lesser of parts (a) and (b) that is required for any seismic load case for a shear wall design. Since it is less than the scale factors for any of the three reinforced masonry SFRS categories, we can conclude in this case that the shear must be scaled up by 50% (see previous section).

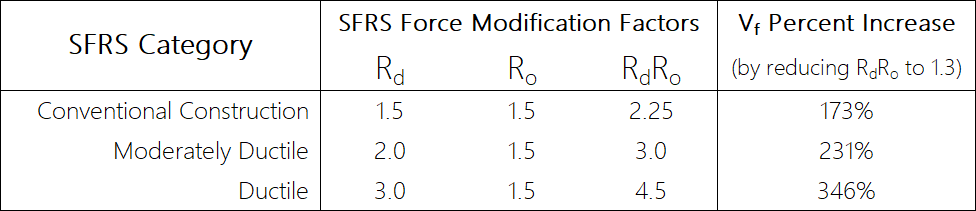
For demonstration sake, replacing the product of R_dR_o with 1.3, the initial factored shear force experienced at the critical section can be multiplied by the ratio of R_dR_o to 1.3. In this example, the seismic shear in part (b) is shown below:

V_f,seismic = V_f x R_dR_o/1.3 = 250 kN x (2.25 / 1.3) = 432.7 kN [Does not govern]

Since V_f,seismic in part (b) is less than the value of part (a), only the lesser limit be taken as the factored in-plane shear resistance that the shear wall must be designed to resist, taking into account seismic considerations.

More information regarding part B requirements can be found on the main V_f,seismic post here.

It should also be noted that different SFRS types reference different moment resistances so the percentages shown cannot be directly compared to one another. Moment resistance, nominal moment resistance, and probable moment resistance each have different values and will result in different degrees by which V_f is scaled to consider seismic effects.

To return to the main V_f,seismic topic which includes an explanation for the second limit (part B), as well as the differences that arise from using other SFRS categories, click here. A multi-storey example covering the same topic as this post is also linked below for further reading.

Additional reading: V_f,seismic calculation example for Multi-Storey Shear Wall