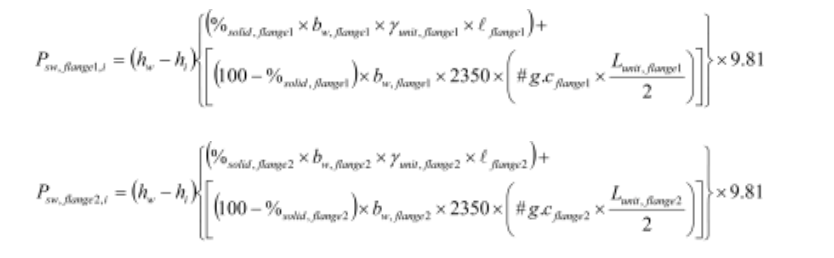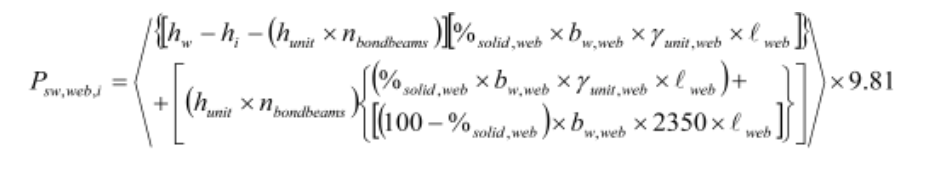Shear Wall Self-Weight
Explaining how MASS determines self-weight for a shear wall element
Note that while the information contained within this article is still current, it is also accessible in a more user friendly format in the Masonry Self-Weight page linked here.
MASS determines the self-weight of shear walls,Psw, by adding the weight of the web and the weight of the flanges, if applicable. The program differentiates if the shear wall is not grouted, partially grouted, or fully grouted; and, if the web has bond beams or not. The total weight is calculated at each critical section (starting form the bottom of the shear wall).
The program first determines the weight of the flanges (if any). For flanges that are not grouted, only the weight of the units is considered; and it is calculated using the solid percentage of the unit per wall length as follows:
Psw, flange1,I = (hw – hi) [%solid,flange1 x bw,flange1 x γunit,flange2 x ℓflange2] x 9.81
Psw, flange2,I = (hw – hi) [%solid,flange2 x bw,flange2 x γunit,flange2 x ℓflange2] x 9.81
Where, hw is the height of the shear wall, hi is the height from the base of the wall to the critical course, bw,flange1, and, bw,flange2 are the thicknesses of each flange , ℓflange1 and ℓflange2 are the actual lengths of each flange, γunit,flange1 and γunit,flange2 are the density of the units in each flange, and finally, %solid,flange1 and %solid,flange2 are the percentages of the volume of the block that is solid material (as opposed to the cells) of each flange.
For fully grouted flanges, the self-weights of flange 1 and flange 2 are calculated as follows:
For partially grouted walls, the self-weight of flange 1 and flange 2 are calculated as follows:
For a web that is not grouted, if there are no bond beams, the program uses the same approach used for a flange that is not grouted. If the web contains bond beams, the program subtracts the height of the bond beams from the not grouted wall weight calculation, and then it adds the weight of the bond beams (weight of units plus the weight of the grout), as follows:
Psw, web,I = (hw – hi) [%solid,web x bs,web x γunit,web x ℓweb] x 9.81
Where, hunit is the height of the bond beam unit, nbondbeams is the number of bond beams in the web, bw,web is the is the thickness of the web, ℓwed is the actual length of the web, γunit is the density of the units in the web, and finally, %solid is the percentages of the volume of the block that is solid material (as opposed to the cells).
For a fully grouted web, the program uses the same approach used for the fully grouted whether there are bond beams or not:
For a partially grouted web, if there are no bond beams, the program uses the same approach used for the partially grouted flanges:
If there are bond beams, the program subtracts the height of the bond beams from the partially grouted wall weight calculation, and then it adds the weight of the bond beams (weight of units plus the weight of the grout):
Notice, the weight of the reinforcing bars (vertical or horizontal) is not included.