P-M Interaction Diagram

Providing a deep dive into the specifics on how the Interaction Diagram is generated

 

After achieving a successful axial, moment and deflection design, the program creates an axial resistance P_r vs. moment resistance M_r  diagram. The calculation procedure and the curves displayed in the P-M diagram depend on whether the wall is reinforced or not, and whether the masonry is hollow, partially grouted or fully grouted.

 In the case of partially grouted and fully grouted walls, MASS provides separate curves depending on whether or not the effect of the grout is included (hollow walls do not contain grout, so this distinction is not made). When the grout is included, the compressive strength,f’_m, is reduced. Thus, when the compression zone is just outside the first face shell it is possible that the moment resistance is smaller when the grout is included than when it is not. In practice, adding grout does not reduce the moment capacity of the wall; hence, it is permissible to ignore the effect of grout if this is advantageous. Providing separate curves also allows users to compare personal calculations with those in the program.

MASS also provides an envelope curve, based on the grout ignored and grout included curves drawn. The envelope curve indicates the bounds of acceptable P_r and M_r combinations, that is, those that cannot be exceeded by the combination of P_r and M_r that appears in the program.

 In the P-M interaction diagram, and for every load combination, the program displays points representing the axial force (P_f, M_fp), and the axial force and the total (magnified) moment (P_f,M_f,Total)  . A thin horizontal black line connects the two points, providing users with a clear picture of the magnification effect.

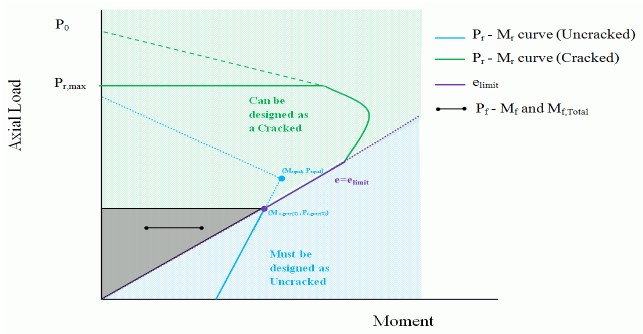
P-M Interaction Diagram (Unreinforced Masonry)

The moment resistance M_r is determined and plotted for incremented values of the axial resistance P_r. The moment resistance calculations vary depending on whether the wall is designed as an uncracked or a cracked section.

The P-M interaction diagram for unreinforced masonry walls is created in three separate stages. The first stage, where the wall must remain uncracked (the curve is under the e_limit line). The second stage or middle stage is governed by the e_limit line, and how this line intersects with previous lines (design stages one and three). The third stage, where the wall can be designed as a cracked section (the curve is above the e_limit line) and the moment resistance is calculated using the equivalent rectangular stress block. The following sections describe the methodology used for each situation.

Uncracked Moment Resistance (Tensile)

The uncracked tensile moment resistance line intersects with the e_limit line, and the corresponding axial load resistance (P_grey1(T)   or P_grey2(T)  ) is less than the axial load resistance when the tensile moment resistance is equal to the compressive moment resistance (P_equal1 or P_equal2). See Figure 0‑1: Uncracked Moment Resistance (Tensile). The program plots the uncracked moment resistance up to the e_limit line, at the intersecting point (P_grey1(T),P_grey2(T))  or (M_r,grey2(T), P_r,grey2(T)).

Figure 1: Uncracked Moment Resistance (Tensile)

Uncracked Moment Resistance (Compressive)

The e_limit line intersects the compressive moment resistance line, and the corresponding axial load resistance (P_r,grey1(c))   or P_r,grey2(c)) is greater than the axial load resistance when the tensile moment resistance is equal to the compressive moment resistance (P_equal1  or P_equal2). See Figure 0‑2: Uncracked Moment Resistance (Compressive)‑.

Since, the program uses a safety factor ∅_linear,to ensure that the uncracked moment resistance remains in a region that is governed by linear behaviour; the program plots the uncracked moment resistance up to where the tensile moment resistance is equal to the compressive moment resistance (P_equal1 or P_equal2). At this point, to avoid underestimating the capacity of the wall, a vertical line is drawn up to the e_limit line, at the point

(M_r,grey1(c), P_r,grey1(c))  or M_r,grey2(c), P_{r,grey 2(c)}

.

Figure 2: Uncracked Moment Resistance (Compressive)

Cracked Moment Resistance (Tensile)

 At the point where the wall is no longer required to remain uncracked, (M_r,grey(T), P_r,grey(T))   or (M_r,grey(c), P_r,grey(c))   , the program calculates the moment resistance of the cracked wall using the equivalent rectangular stress block. The neutral axis depth, C₁ and C₂, is determined for incremented values of the axial resistance, P_r1 and P_r2. With the neutral axis depth, the corresponding moment resistance, M_r1  and, M_r2, is determined. This moment resistance value is later compared to the one along the  e_limit line (for the same axial resistance). The program then plots the lesser of the two moments.

Cracked Moment Resistance (Compressive)

At the point where the moment resistance along the  e_limit line is no longer the smaller value (for the same axial resistance). The program continues calculating the moment resistance, M_r1  and, M_r2, of the cracked wall using the equivalent rectangular stress block, C₁ , and, C₂.

Grey zone

It is possible for the factored loads (P_f, M_f,Total)  to fall inside the cracked portion of the P-M diagram, but at the same time have a corresponding uncracked moment resistance. To ensure that the program does not skip over a possible solution by assuming the design fails, when in fact the uncracked section provides enough resistance; the program uses the grey zone.

The grey zone is located above the  e_limit line, and extends up to the axial resistance where the  e_limit line intersects with the uncracked curve, P_grey1 or P_{grey 2}. Note that shaded grey zone is not displayed in the P-M diagram; it is shown in Figure 0‑1: Uncracked Moment Resistance (Tensile)‑ and Figure 0‑2: Uncracked Moment Resistance (Compressive)‑ for explanatory purposes only.

When the factored loads fall within the grey zone, the program verifies both the uncracked and cracked moment resistance before establishing the success or failure of a design.

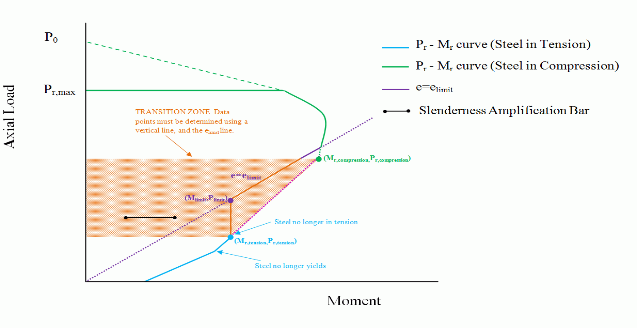
P-M Interaction Diagram (Reinforced Masonry)

 The axial resistance P_r and the moment resistance M_r are determined and plotted for incremented values of the neutral axis depth c. The neutral axis depth begins with c=1mm and is incremented up by 1 mm with each iteration, terminating when the compression zone is equal to the thickness of the block (when β_1c=ℓ_w).

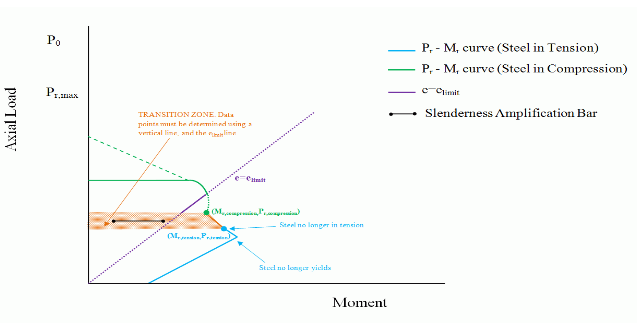
MASS does not account for reinforcement in compression in the moment resistance calculations, since tying bars in walls is not easily accomplished. Consequently, in the case where compression zone depth is equal to the depth of the reinforcement, c=d₁, where the steel transitions from being in tension (M_r,tension, P_{r, tension}) to being in compression (M_{r,compression},P_{r,compression}), the moment resistance varies considerably upon the smallest increment of, c. This results in missing moment resistance and axial resistance data points in between this transition zone.

In order to create a smoother transition in the P-M diagram, while maintaining a conservative design, the program takes special design considerations depending on the case in which the transition zone is encountered.

Case 1

Case 1 occurs when the transition zone points (M_r,tension, P_{r, tension}) and (M_{r,compression}, P_{r,compression}) fall below the  e_limit line, and these point connect to form a line with a positive slope (Figure 0‑3: Transition Zone (Case 1)‑).

In order to obtain data points for the transition zone, the program divides the zone into two sections. First, a vertical line is drawn from (M_r,tension, P_{r, tension}) to the  e_limit line. And secondly, the  e_limit line is extended to(M_{r,compression}, P_{r,compression}), where the wall is treated as unreinforced.

Figure 3: Transition Zone (Case 1)

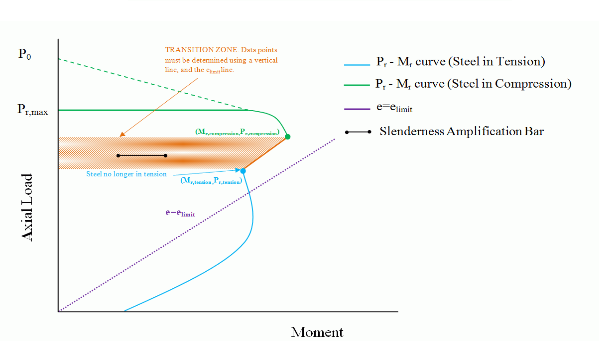
Case 2a

Case 2a occurs when both transition points, (M_r,tension, P_{r, tension}) and

(M_{r,compression}, P_{r,compression}), fall above the e_limit line (see Figure 0‑4: Transition Zone (Case 2a)‑).

In order to obtain data points for the transition zone, the program draws a line connecting the points (M_r,tension, P_{r, tension}) and (M_{r,compression}, P_{r,compression}). Note, that this methodology is applied independent of whether the (M_{r,compression}, P_{r,compression}) is to the left or right of (M_r,tension, P_{r, tension})   , as long as both points are above the e_limit line. The connecting line is governed by the following equation:

Figure 4: Transition Zone (Case 2a)

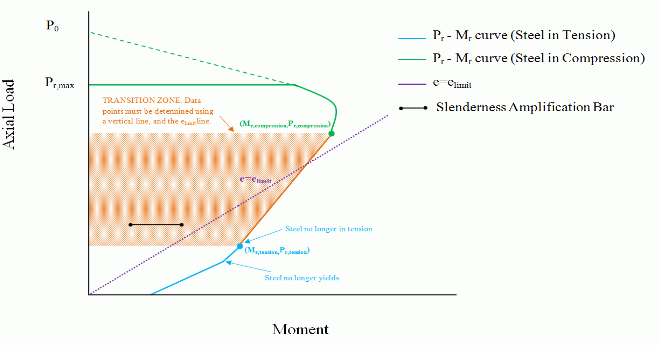
Case 2b

This case occurs when the steel in tension point (M_r,tension, P_{r, tension})  falls above the  e_limit line, and the steel in compression point (M_{r,compression}, P_{r,compression}) falls below the  e_limit line (see Figure 0‑5: Transition Zone (Case 2b)‑). The slope of the line obtained when connecting the transition points is positive.

For this particular case, since (M_{r,compression}, P_{r,compression}) falls below the  e_limit line, the program is concerned  with the unreinforced wall cracking past the permitted limit (dictated by  e_limit). To account for this, the program determines the moment resistance from the linear equation used in Case 2a  and compares it to the moment resistance along the  e_limit line, calculated as follows:

M_r=P_re_limit

The smaller of the two moment values is used.

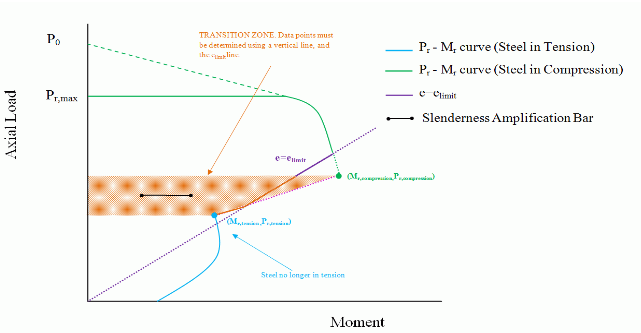Figure 5: Transition Zone (Case 2b)

Case 3a

Case 3a occurs when steel in tension point (M_r,tension, P_{r, tension}) falls below the  e_limit line, and the steel in compression point (M_{r,compression}, P_{r,compression}) falls above the  e_limit line (see Figure 0‑6: Transition Zone (Case 3a)‑). The slope of the line obtained when connecting the transition points is positive.

In order to obtain data points for the transition zone, the program draws a line connecting the points (M_r,tension, P_{r, tension}) and (M_{r,compression}, P_{r,compression}). The connecting line is the same linear line provided in Case 2a.

Figure 6: Transition Zone (Case 3a)

Case 3b

Case 3b occurs when both transition points, (M_r,tension, P_{r, tension}) and (M_{r,compression},P_{r,compression}), fall below the  e_limit line (see Figure 0‑7: Transition Zone (Case 3b)‑). The slope of the line obtained when connecting the transition points is negative.

In order to obtain data points for the transition zone, the program draws a line connecting the points (M_r,tension, P_{r, tension})    and (M_{r,compression}, P_{r,compression}). The connecting line is governed by the equation shown in Case 2a.

Figure 7: Transition Zone (Case 3b)

Continue Reading: P M Interaction Diagram Shear